「論理回路とその設計」 演習問題【9】
| 表1 |
| 10進数 |
BCD符号 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
1 |
| 2 |
0 |
0 |
1 |
0 |
| 3 |
0 |
0 |
1 |
1 |
| 4 |
0 |
1 |
0 |
0 |
| 5 |
0 |
1 |
0 |
1 |
| 6 |
0 |
1 |
1 |
0 |
| 7 |
0 |
1 |
1 |
1 |
| 8 |
1 |
0 |
0 |
0 |
| 9 |
1 |
0 |
0 |
1 |
[A] 1桁の10進数("0","1",…,"8","9")を4ビットの2進数(各ビットの重み:最上位から最下位へ10進数で8-4-2-1)を自然に用いて表す符号表現を「BCD(Binary Coded Decimal; 2進符号化10進数)符号」という.表1は10進数とBCD符号との対応表である.また,1桁の10進数をNとするとき,上位への桁上げを無視した1桁の10進数(10−N)を「Nの10の補数」(N'と表す,N'=10−N)という.表2はNとN'との対応表である.ここで,Nを4ビットのBCD符号 ABCD(Aが最上位ビット,Dが最下位ビット) で,各Nに対応するN'を4ビットのBCD符号 WXYZ(Wが最上位ビット,Zが最下位ビット)で,それぞれ表す.ABCD を入力,WXYZ を出力とする4入力4出力の組み合わせ回路を設計してみよう.ただし,入力 ABCD が"1010","1011","1100","1101","1110","1111"の6通り(BCD符号ではない)のそれぞれでは,いずれも出力WXYZ は4ビットともすべてドントケア"−−−−"とする.
次の問すべてに答えなさい.論理積(AND)記号"・"は省略可.
(1) 下記の真理値表のW,X,Y,Z列の空白部分を埋めて,真理値表を完成しなさい.
(2) (1)の真理値表から出力W,X,Y,Zのそれぞれを下記の対応するカルノー図に移して,それを用いて出力W,X,Y,Zのそれぞれを2段論理最小化し,最小積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
(3) (2)で求めた出力W,X,Y,Zの各最小積和形のうちで,ファクタリングを用いて多段論理最小化できるものがあれば,それらすべて(の結果)を論理式で示しなさい.
| 表2 |
| N |
N' |
| 0 |
0 |
| 1 |
9 |
| 2 |
8 |
| 3 |
7 |
| 4 |
6 |
| 5 |
5 |
| 6 |
4 |
| 7 |
3 |
| 8 |
2 |
| 9 |
1 |
(4) 次に,入力 ABCD が"0000"の場合の出力WXYZ をすべてドントケア"−−−−"とする場合に,カルノー図を用いて出力W,X,Y,Zのそれぞれを2段論理最小化し,最小積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.解が複数ある場合には,いずれか1つを示せばよい.
(5) (4)の4入力4出力組み合わせ回路をNOTゲートと2入力AND/ORゲートだけで構成して1回路にまとめると,共有(共用)ゲートの存在によってさらなる空間最適化ができるかどうかについて,(4)の解答である論理式を引用することによって具体的に説明しなさい.複数の場合があるときは,それら相互が両立するかどうかについても述べなさい.
| 表3 |
| |
X |
Y |
Z |
| p |
0 |
0 |
0 |
| q |
0 |
0 |
1 |
| r |
0 |
1 |
0 |
| s |
0 |
1 |
1 |
| t |
1 |
0 |
0 |
[B] 1ビット入力 I をクロック(ビットタイム)ごとにチェックして,"0"か"1"が3ビット以上引き続いて入力している((1→)0→0→0→…あるいは(0→)1→1→1→…,→は入力の時間順序「先入力→後入力」を示す)状態を検出する同期式順序回路を設計してみよう.この順序回路の状態は, p:初期(リセット)状態; q:初期状態の次に"0"が1ビットだけ入力した状態; r:初期状態の次に"1"が1ビットだけ入力した状態; s:初期状態の次から"0"が2ビット以上引き続いて入力している(0→0→…)状態; t:初期状態の次から"1"が2ビット以上引き続いて入力している(1→1→…)状態;の5状態とする.【たとえば,q 状態で,次に"0"が入力されると s 状態に,"1"が入力されると初期状態 p に,それぞれ遷移する.また,t 状態で,次に"0"が入力されると初期状態 p に,"1"が入力されると同じ t 状態に,それぞれ遷移する.】さらに, q,r,s,t の4状態では,直前の入力が"0"か"1"かが決まっている(分かっている)ので,それと異なる論理値が入力されると初期状態 p へ戻る(リセットである,リセットを引き起こした入力は以降の状態遷移に何ら影響しない).設計する順序回路では,出力は省略し,状態遷移すなわちフリップフロップ(FF)の入力条件式だけを考える.同期式順序回路であるので,状態遷移(カウントダウン)はクロックに同期することを前提とするが,解答(論理式や回路図)では,クロックは無視し省略しなさい.次の問すべてに答えなさい. 論理積記号"・"は省略可
(1) この順序回路の状態遷移図を状態記号 p,q,r,s,t を使用して書きなさい.解答は下記の状態(ノード)間に状態遷移を示す矢印を引き,その矢印にその状態遷移を起こす入力の論理値("0"か"1")をラベルとして付けることによって示しなさい.各状態(ノード)から出る矢印は2本であることに注意しなさい.また,上記の例(【 】部分,q 状態と t 状態)の状態遷移は記入済みである.
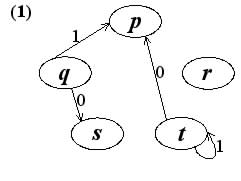
(2) (1)をもとにして,この順序回路の状態遷移表を状態記号 p,q,r,s,t を使用して書きなさい.解答は下記の「記号による」状態遷移表の次状態列(I=0とI=1の2列)の空欄を埋めることで示しなさい.また,上記の例(【 】部分)の状態遷移は記入済みである.
(3) この順序回路は5状態であるので,3個のFF(その状態=出力をそれぞれ X,Y,Z とする)を用いて設計できる.そして,p,q,r,s,t の5状態を3個のFF X Y Z で表せる8状態のうちの5状態に表3のように割り当てる.割り当てのないXYZ="101","110","111"の3通りのそれぞれには状態遷移しない.すなわち,これらの3状態に対応する次状態 X+ Y+ Z+ はドントケア"−−−"とする.この状態割り当てにしたがって,現状態と入力をラベルとする拡大状態遷移表へ(2)の状態遷移表を展開しなさい.解答は下記の拡大状態遷移表の次状態 X+,Y+,Z+ の各列の空欄を埋めなさい.
(4) この順序回路をD-FFによって構成する.(3)で作った拡大状態遷移表の右側に連結してある DX,DY,DZ 列の空欄を埋めることによって,拡大入力要求表として完成しなさい.D-FFの入力要求表は右記してある.
| 現 状態 |
次状態 |
| I=0 |
I=1 |
| p |
|
|
| q |
s |
p |
| r |
|
|
| s |
|
|
| t |
p |
t |
(5) (4)の DX,DY,DZ 列を下記の対応するカルノー図に写し,DX,DY,DZ のそれぞれを2段論理最小化してそれぞれの最小積和形論理式を求めなさい. カルノー図による操作はすべて解答として明記しなさい.
(6) 各FFのD入力を2段論理最小化した(5)を順序回路(ただし,3個のD-FF以外にはNOTゲートと2入力(AND/OR)ゲートだけで構成する)としてまとめると,共有(共用)ゲートの存在によってさらなる空間最適化ができるかどうかについて,(5)の解答である論理式を引用することによって具体的に説明しなさい.
(7) (5)で求めた各FFのD入力 DX,DY,DZ の各最小積和形のうちで,ファクタリングを用いて多段論理最小化できるものがあれば,それらすべて(の結果)を論理式で示しなさい.

