「論理回路とその設計」 演習問題【1】
A.4人(P,Q,R,S) の投票者が可"1"か否"0"を各1票ずつ投票し、「可」とする票と「否」とする票の多数の方を1ビットの票決(可"1"か否"0")とする可否投票の票決を判定する論理関数がある。ただし、可否が2票ずつの同数の場合の可否決定ルールは、以下の
[a] [b] [c] の3通りがあり、それぞれのルールに従う票決を Ma,
Mb, Mc とする。これらの論理関数を各々組み合わせ論理回路として実現したい。次の(1)〜(7)の各問に答えよ。なお、投票に際しては棄権や白票は無いものとする。
【可否同数の場合の可否決定ルール】
[a] P の票に従う(P が「決定権」を持つ)。
[b] P の票が否"0"の場合は否"0"、P の票が可"1"の場合はドントケア(don't
care)"−"とする(P が「拒否権」を持つ)。
[c] ドントケア(don't care)"−"とする(可否を決めない)。
(1) P, Q, R, S と
Ma, Mb, Mc の論理関係を真理値表として示せ。
(2) (1)で求めた真理値表をもとに、カルノー図を用いて、P,
Q, R, S を論理変数とする論理関数 Ma を最簡積和形論理式として求めよ。最簡形が複数ある場合はそれらすべてを示せ。
(3) (2)と同様にして、論理関数Mb
を最簡積和形論理式として求めよ。最簡形が複数ある場合はそれらすべてを示せ。
(4) 同様にして、論理関数Mc
を最簡積和形論理式として求めよ。最簡形が複数ある場合はそれらすべてを示せ。
(5) (2)で求めた積和形論理関数 Ma(P,Q,R,S)
を、P, Q, R, S を入力、Ma を出力とするAND/OR回路(AND/OR/NOTの基本論理ゲートだけから構成される回路;ただし、ANDゲートとORゲートは3以上の多入力も許す)として示せ。
(6) 1個のn入力基本論理ゲートは(n−1)個の2入力基本論理ゲートとして換算する(ただし
n≧2)ものとして、(5)で求めたAND/OR回路よりもさらに空間最適化された(ゲートの総数がより少ない)AND/OR回路は有るか。無いならその理由、有るならそのAND/OR回路及びその回路を表す論理式を、それぞれ示せ。
(7) (6)で「無い」とした場合は(5)で、「有る」とした場合は(6)で、それぞれ構成したAND/OR回路をNAND回路に変換して示せ。ただし、2入力NANDゲートだけが使えるものとする。
B.3個のJKフリップフロップ(JK-FF)を用いて、n進カウンタ(ただし、n=5,6,7,8)を同期式の順序回路として設計したい。3個のJK-FFの出力をそれぞれ
QC QB QA とし、3個のFFの出力の並び
QC QB QA がこの順で最上位ビットから最下位ビットのカウンタの3ビット状態(出力)である。例えば、8進カウンタとは、QC
QB QA が 000 → 001 → 010 → 011
→ 100 → 101 → 110 → 111 → 000 → …(以降は同じ繰り返しのため省略)
という8つの状態をこの順で遷移することを繰り返す。また、5進カウンタとは、QC
QB QA が 000 → 001 → 010 → 011
→ 100 → 000 → … という5つの状態をこの順で遷移することを繰り返し、残りの3つの状態:
101 , 110 及び 111 はドントケア"−"である。
(1) まず、8進カウンタを構成する。右のJK-FFの入力要求表(Q
から Q+ へ状態遷移させるために必要な J K 入力信号の論理値を示す表)を用いて拡大入力要求表を作成し、それをカルノー図に写すことによって、各JK-FFの
J K 入力 JC1 , KC1 , JB1
, KB1 , JA1 , KA1
すべてについて、各FFの出力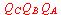 およびその否定出力
およびその否定出力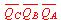 を論理変数とする最簡積和形論理式として示せ。
を論理変数とする最簡積和形論理式として示せ。
(2) 同様にして、7進カウンタを構成する各JK-FFの入力 JC2
, KC2 , JB2 , KB2
, JA2 , KA2 すべてを最簡積和形論理式として示せ。
(3) 同様にして、6進カウンタを構成する各JK-FFの入力
JC3 , KC3 , JB3 ,
KB3 , JA3 , KA3 すべてを最簡積和形論理式として示せ。
(4) 同様にして、5進カウンタを構成する各JK-FFの入力
JC4 , KC4 , JB4 ,
KB4 , JA4 , KA4 すべてを最簡積和形論理式として示せ。
(5) (1)〜(4)で構成した8/7/6/5進カウンタのうち、回路の空間規模(基本論理ゲートの総数)が最小のカウンタはどれか。また、その回路をJK-FFと基本論理ゲート(AND/OR/NOTゲート)で構成せよ。
(6) (1)〜(4)で構成した8/7/6/5進カウンタのうち、回路の空間規模(基本論理ゲートの総数)が最大のカウンタはどれか。また、その回路をJK-FFと2入力NANDゲートで構成する場合、JK-FF以外に2入力NANDゲートはいくつ必要か、理由を添えて答えよ。
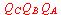 およびその否定出力
およびその否定出力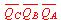 を論理変数とする最簡積和形論理式として示せ。
を論理変数とする最簡積和形論理式として示せ。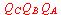 およびその否定出力
およびその否定出力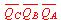 を論理変数とする最簡積和形論理式として示せ。
を論理変数とする最簡積和形論理式として示せ。