[A] A(第3ビット，最上位)，B(第2ビット)，C(第1ビット)，D(第0ビット，最下位)の4ビットの入力を持つ組み合わせ回路を設計してみよう．次の問すべてに答えよ．

(1) 「A,B,C,Dの4ビットの入力のうち，最上位の"1"は第nビット(n=0,1,2,3)か？」を2ビットの出力X,Yとして示す論理回路を「4-to-2 プライオリティエンコーダ」という．n=0,1,2,3の時，この順で，XY="00","01","10","11"として示す．例えば，ABCD="0101"であれば，最上位の"1"はBの第2ビットであるからXY="10"を出力する．また，ABCD="1111"であれば，XY="11"となる．下記の真理値表のX,Y列を完成させよ．ただし，ABCD="0000"の場合の出力はドントケア(XY="−−")とする．

(2) (1)を下記の対応するカルノー図に写し，XとYの最簡積和形論理式を求めよ．

(3) 「 A,B,C,Dの4ビットの入力のうち，"0","1"のいずれか多い方」を1ビットの出力Zとして示す論理回路を「多数決回路」という． 下記の真理値表のZ列を完成させよ．ただし，"0","1"のいずれも2ビットずつで同じ場合の出力はドントケア(Z="−")とする．

(4) (3)を下記の対応するカルノー図に写し，Zの最簡積和形論理式を求めよ．最簡積和形が複数存在する場合は，そのすべてを示せ．

(5) 今度は(3)でドントケアとした「"0","1"のいずれも2ビットずつで同じ場合(＊)」の決着を付けるために，Aに"4"，Bに"3"，Cに"2"，Dに"1"の重みを与え，＊の場合には，重みを付けて計算し，重い方の論理値("0","1"のいずれか)を出力Z'とする．例えば，ABCD="0101"では，"0"の重みが"6"で，"1"の重みが"4"であるから，Z'="0"である． 下記の真理値表のZ'列を完成させよ．ただし，重みも同じ場合の出力はドントケア(Z'="−")とする．

(6) (5)を下記の対応するカルノー図に写し，Z'の最簡積和形論理式を求めよ．また，この論理式が表す論理回路は何個の2入力基本(AND/OR)ゲートで構成できるか論理式より求めよ．ただし，回路を構成するゲート総数の勘定にNOTゲートは入れない．

(7) (6)のような積和形論理式が表す論理回路は多入力(3入力以上)基本ゲートを使用しても良いという条件で構成すると高々2段(レベル)の組み合わせ回路(AND-OR回路)となり，これは時間最適化された(高々2段以下の)論理回路のうちでさらに空間最適化された論理回路を与える．それでは，この「時間最適化する」という制約をはずすと，(6)はさらに空間最適化できるか？　できるならば，その論理式を示し，それが表す論理回路は何個の2入力基本(AND/OR)ゲートで構成できるか論理式より求めよ． ただし，回路を構成するゲート総数や段数の勘定にNOTゲートは入れない．

(8) (7)で示した論理式を表す論理回路(AND/OR回路)を2入力基本ゲートで構成し，さらに，それを2入力NANDゲートだけで構成する論理回路(NAND回路)に変換し，その回路図を示せ．また，このNAND回路は何個のNANDゲートで構成できるか示せ．  

[B] 「50円/100円/500円の各硬貨を受け付けて，150円のハンバーガと(必要ならば)釣銭を出す」簡易自動販売機を順序回路として設計してみよう．次の問すべてに答えよ．ただし，入力，状態，出力及びそれぞれの制約条件を次のように定めておく． また，ビットタイム(クロック)ごとに，硬貨が投入(入力)され，出力の有無がチェック(必要ならば出力)される「同期式順序回路」として構成する．

［入力］

• 投入できる硬貨は，50円硬貨 i₁；100円硬貨 i₂；500円硬貨 i₃；とラベル付けした3種類とする．
• 入力線は XY の2ビットとし， i₁：XY="01"； i₂：XY="10"； i₃：XY="11"；で表す．

• ハンバーガ(代金：150円) hと釣銭 c とラベル付けする．
• 投入硬貨の合計が150円以上になった時点で出力(ハンバーガは必ず，釣銭は必要時)して初期状態に戻る．「釣銭だけの出力」は無い．(＊)
• 釣銭は「『有無』のみを示せば良い(額は不問)」とする．
• 出力線は HC の2ビットとし，h出力の時 H="1"；c出力の時 C="1"；その外はHCとも"0"；と表す．（＊によって，HC="01"は生じない．）

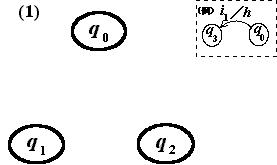
• 状態を投入硬貨の合計(累積)金額で表すと，0円分累積(初期状態) q₀；50円分累積 q₁；100円分累積 q₂；とラベル付けた3状態で良い．
• 状態は PQ の2個のフリップフロップ(FF)で表し，q₀：PQ="00"；q₁：PQ="01"；q₂：PQ="10"；とする．PQ="11"はドントケア("−")である．

(1) 入力による3状態間の遷移と出力を下図の状態遷移図によって示せ．ただし，状態遷移は下記のように状態(ノード)間に引く矢印のラベルとして「入力／出力」と表し，入出力ともラベル(英小文字)で示せ． h,cいずれも出力されない時のラベルは"×"(ラベル"×"では HC="00")とせよ．

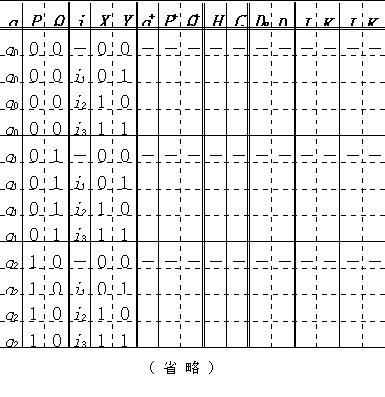
(2) (1)を写すことによって，下記の状態遷移表の q⁺,P⁺,Q⁺,H,C の各列を埋めよ．(この状態遷移表では，PQ="11"のドントケアの4行は省略してある．)

(3) (2)を下記の対応するカルノー図に写し，出力H,Cの各最簡積和形論理式を求めよ．最簡積和形が複数存在する場合でもいずれか1つを示せば良い．

(4) (3)の出力H,C は，併せて何個の2入力基本ゲート(AND/ORゲート)による組み合わせ回路として構成できるか示せ． この時，空間最適化を図るものとする． ただし，FFやNOTゲートは勘定から除き，空間最適化もH,Cを構成するためのゲートだけで行う．

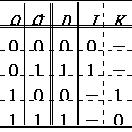
(5) まず，PQにD-FFを使用する論理回路を作ろう．PとQのD入力であるD_P及びD_Qとして，(2)の状態遷移表の右側のD_PとD_Qの各列を埋めて，拡大入力要求表を作れ．（D-FFの入力要求表は右記参照）

(6) (5)を下記の対応するカルノー図に写し，D_PとD_Qの各最簡積和形論理式を求めよ．

(7) (6)は，何個の2入力基本ゲート(AND/ORゲート)によって構成できるか示せ．この場合にも，空間最適化を図るものとする． ただし，回路を構成するゲート総数の勘定にFFやNOTゲートは入れない．

(8) 次に，PQにJK-FFを使用する論理回路を作ろう．PとQのJK入力であるJ_P.K_P及びJ_Q.K_Qとして，(2)の状態遷移表の右側のJ_P.K_P.J_Q.K_Qの各列を完成して，拡大入力要求表を作れ． （JK-FFの入力要求表は右記参照）

(9) (8)を下記の対応するカルノー図に写し，J_P.K_P.J_Q.K_Q の各最簡積和形論理式を求めよ．