「論理回路とその設計」 演習問題【10】
| 表1 |
| Y X |
0 |
1 |
−1 |
| 0 |
0, 0 |
1, 0 |
1, −1 |
| 1 |
1, 0 |
0, 1 |
0, 0 |
| −1 |
1, −1 |
0, 0 |
0, −1 |
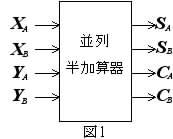
[A] 2進数値の1桁を"0","1","−1"の3値で表す方式を「冗長2進表現」という.この冗長2進表現数値の1桁どうしの半加算器(被加数と加数を並列・同時に入力するので「並列半加算器」という)を最適化設計してみよう.この半加算器は,被加数Xと加数Yとを入力として,その桁での和Sと上位への桁上げCを出力とする組み合わせ回路であり,X+Y=S, C を表1(行が被加数のX値,列が加数のY値,交差するマス目にある"S, C"がこの順で和のS値と桁上げのC値を示す )の組み合わせにしたがって計算・出力する.たとえば,X=Y=−1 ならば,S=0, C=−1 である.また,設計する論理回路では,[冗長2進表現の1桁数値である"0"を"00","1"を"01","−1"を"11"のそれぞれ2ビットの論理値(2ビットコード)で表現(*)]する.たとえば,X=1は,XA=0, XB=1 の2ビット(コード)で表現する.したがって,最適化設計する論理回路は,図1に示すように,XA,XB,YA,YBを入力,SA,SB,CA,CBを出力とする4入力4出力組み合わせ回路となる.ただし,入力XA=1, XB=0 あるいは YA=1, YB=0 の場合は,4ビットの出力SA,SB,CA,CBともすべてドントケア"−"とする. 次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
 (1) まず,表1を下記の真理値表のS,C列の対応部分に写した後,上記の[コード化規則(*)]にしたがって,SA,SB,CA,CBの空白部分を埋めて,真理値表を完成しなさい.
(1) まず,表1を下記の真理値表のS,C列の対応部分に写した後,上記の[コード化規則(*)]にしたがって,SA,SB,CA,CBの空白部分を埋めて,真理値表を完成しなさい.
(2) (1)の真理値表から出力SA,SB,CA,CBのそれぞれを下記の対応するカルノー図に写して,それを用いて出力SA,SB,CA,CBのそれぞれを2段論理最小化し,最小積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
(3) (2)の2段論理最小化した4入力4出力組み合わせ回路をNOTゲートとAND/ORゲートだけで構成して1回路にまとめると,共有(共用)ゲートの存在によって(「2段」という時間最適化を保持したまま)さらなる空間最適化ができるかどうかについて,(回路図を示すのではなく)(2)の解答である論理式を引用することによって具体的に説明しなさい.
(4) 実は,(3)で調べた「共有(共用)ゲートが存在するかしないか」は,(2)で作ったカルノー図(2段論理最小化操作後)を見れば,すぐに分かる.カルノー図によって共有(共用)ゲートの有無を調べる方法について説明しなさい.
(5) (2)で求めた出力SA,SB,CA,CBの各最小積和形のうちで,ファクタリングを用いて多段論理最小化できるものがあれば,それらすべて(の結果)を論理式で示しなさい.
(6) 実は,(5)で調べた「ファクタリングできるかできないか」も,(2)で作ったカルノー図(2段論理最小化操作後)を見れば,すぐに分かる.カルノー図によってファクタリングの可/不可を調べる方法について説明しなさい.
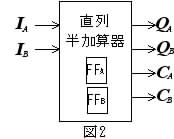 [B] [A]と同様に冗長2進表現した1桁数値を,今度は,ビットタイムごとに逐次的に(時間系列で順々に)入力して,時間系列で連続する2個の冗長2進表現数値の1桁どうしの半加算器(直列・逐次入力するので「直列半加算器」という)を最適化設計してみよう.この直列半加算器は,現状態Qを被加数,入力Iを加数として加算し,次状態Q+をその桁での和,出力Cを上位への桁上げとし,Q+I=Q+, C を表1の組み合わせ(表1での,XをQに,Y をIに,SをQ+にそれぞれ読み替える)にしたがって計算・状態遷移・出力する順序回路である.たとえば,[Q=I=1 ならば,Q+=0, C=1 (**)]である.また,この順序回路では,[A]と同様に,冗長2進表現の1桁数値で示せる状態"0"を"00","1"を"01","−1"を"11"のそれぞれ2ビットの論理値(2ビット,2個のフリップフロップ(FF)でこの順で"QA QB")で表現し,これらをそのままこの順序回路そのものの状態・出力(2ビット)とする.ただし,状態"10"は不使用でドントケアとする.たとえば,Q=−1 は,QA=1, QB=1 の2ビット(コード)で表現する.したがって,最適化設計する論理回路は,図2に示すように,IA, IBを入力,QA,QBを状態(出力も兼ねる),CA,CBを出力とし,2個のFFA, FFB(それぞれのFF状態(=FF出力)がQA,QB)を備える2入力4出力順序回路となる.ただし,QA=1, QB=0 はドントケア状態"−"であるから,論理設計する順序回路は不完全指定順序回路(2ビット状態(2個のFF)で表現できる4状態のうち3状態しか使用しない)である.また,入力IA=1, IB=0 の場合の次状態QA+, QB+および出力CA, CBはドントケア"−"とする.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
[B] [A]と同様に冗長2進表現した1桁数値を,今度は,ビットタイムごとに逐次的に(時間系列で順々に)入力して,時間系列で連続する2個の冗長2進表現数値の1桁どうしの半加算器(直列・逐次入力するので「直列半加算器」という)を最適化設計してみよう.この直列半加算器は,現状態Qを被加数,入力Iを加数として加算し,次状態Q+をその桁での和,出力Cを上位への桁上げとし,Q+I=Q+, C を表1の組み合わせ(表1での,XをQに,Y をIに,SをQ+にそれぞれ読み替える)にしたがって計算・状態遷移・出力する順序回路である.たとえば,[Q=I=1 ならば,Q+=0, C=1 (**)]である.また,この順序回路では,[A]と同様に,冗長2進表現の1桁数値で示せる状態"0"を"00","1"を"01","−1"を"11"のそれぞれ2ビットの論理値(2ビット,2個のフリップフロップ(FF)でこの順で"QA QB")で表現し,これらをそのままこの順序回路そのものの状態・出力(2ビット)とする.ただし,状態"10"は不使用でドントケアとする.たとえば,Q=−1 は,QA=1, QB=1 の2ビット(コード)で表現する.したがって,最適化設計する論理回路は,図2に示すように,IA, IBを入力,QA,QBを状態(出力も兼ねる),CA,CBを出力とし,2個のFFA, FFB(それぞれのFF状態(=FF出力)がQA,QB)を備える2入力4出力順序回路となる.ただし,QA=1, QB=0 はドントケア状態"−"であるから,論理設計する順序回路は不完全指定順序回路(2ビット状態(2個のFF)で表現できる4状態のうち3状態しか使用しない)である.また,入力IA=1, IB=0 の場合の次状態QA+, QB+および出力CA, CBはドントケア"−"とする.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
(1) この論理設計では,状態遷移図を作成せずに状態遷移表だけを使用することも可能である.そこでまず,XをQに,Y をIに,SをQ+にそれぞれ読み替えた表1にしたがって,この順序回路の拡大状態遷移表を書きなさい.解答は,読み替えた表1を下記の拡大状態遷移表の次状態Q+列,出力C列のそれぞれに写し,それにしたがってQA+, QB+, CA, CB の空白部分を埋めることで示しなさい. また,[上記の例(**)]の状態遷移は記入済みである.
(2) (1)をもとにして,この順序回路の状態遷移図を書きなさい.解答は解答欄の3状態(ノード)間に状態遷移Q→Q+を示す矢印を引き,その矢印にその状態遷移を起こす入力Iと出力Cをラベル"I/C "として付ける(解答欄の凡例も参照)ことによって示しなさい.ただし,状態Q (Q+),入力I,出力Cはいずれも冗長2進表現の3値("0"か"1"か"−1"のいずれか)で示すものとする.入力は3値なので,各状態(ノード)から出る矢印は3本であることに注意しなさい.また,[上記の例(**)]の状態遷移は記入済みである.
(3) この順序回路をD-FFによって構成する.D-FFの入力要求表は右記した通りであり,D-FFの場合には,(2)で作った拡大状態遷移表のQA +,QB +列がそれぞれDA,DB列となることに注意して,この拡大状態遷移表のDA,DB列および出力CA,CB列を下記の対応するカルノー図に写し,それぞれを2段論理最小化して最小積和形論理式を求めなさい. カルノー図による操作はすべて解答として明記しなさい.
(4) 各FFの入力DA,DBと順序回路の出力CA,CBを2段論理最小化した(3)を順序回路(ただし,2個のD-FF以外にはNOTゲートと多入力(AND/OR)ゲートだけで構成する)としてまとめると,共有(共用)ゲートの存在によってさらなる空間最適化ができるかどうかについて,(5)の解答である論理式を引用することによって具体的に説明し,結果となるAND/OR回路を回路図として示しなさい.
(5) (4)で構成したAND/OR回路をNAND回路(FF以外は多入力NANDゲートだけで構成する)に変換して,回路図として示しなさい.
(6) D-FFはデータ取り込み機能を持つFFであることに注意して,(3)で最適化設計した直列半加算器(順序回路)と[A]の(2)で最適化設計した並列半加算器(組み合わせ回路)とを論理回路として(機能的に)比較し,コメントしなさい.
 (1) まず,表1を下記の真理値表のS,C列の対応部分に写した後,上記の[コード化規則(*)]にしたがって,SA,SB,CA,CBの空白部分を埋めて,真理値表を完成しなさい.
(1) まず,表1を下記の真理値表のS,C列の対応部分に写した後,上記の[コード化規則(*)]にしたがって,SA,SB,CA,CBの空白部分を埋めて,真理値表を完成しなさい. (1) まず,表1を下記の真理値表のS,C列の対応部分に写した後,上記の[コード化規則(*)]にしたがって,SA,SB,CA,CBの空白部分を埋めて,真理値表を完成しなさい.
(1) まず,表1を下記の真理値表のS,C列の対応部分に写した後,上記の[コード化規則(*)]にしたがって,SA,SB,CA,CBの空白部分を埋めて,真理値表を完成しなさい. [B] [A]と同様に冗長2進表現した1桁数値を,今度は,ビットタイムごとに逐次的に(時間系列で順々に)入力して,時間系列で連続する2個の冗長2進表現数値の1桁どうしの半加算器(直列・逐次入力するので「直列半加算器」という)を最適化設計してみよう.この直列半加算器は,現状態Qを被加数,入力Iを加数として加算し,次状態Q+をその桁での和,出力Cを上位への桁上げとし,Q+I=Q+, C を表1の組み合わせ(表1での,XをQに,Y をIに,SをQ+にそれぞれ読み替える)にしたがって計算・状態遷移・出力する順序回路である.たとえば,[Q=I=1 ならば,Q+=0, C=1 (**)]である.また,この順序回路では,[A]と同様に,冗長2進表現の1桁数値で示せる状態"0"を"00","1"を"01","−1"を"11"のそれぞれ2ビットの論理値(2ビット,2個のフリップフロップ(FF)でこの順で"QA QB")で表現し,これらをそのままこの順序回路そのものの状態・出力(2ビット)とする.ただし,状態"10"は不使用でドントケアとする.たとえば,Q=−1 は,QA=1, QB=1 の2ビット(コード)で表現する.したがって,最適化設計する論理回路は,図2に示すように,IA, IBを入力,QA,QBを状態(出力も兼ねる),CA,CBを出力とし,2個のFFA, FFB(それぞれのFF状態(=FF出力)がQA,QB)を備える2入力4出力順序回路となる.ただし,QA=1, QB=0 はドントケア状態"−"であるから,論理設計する順序回路は不完全指定順序回路(2ビット状態(2個のFF)で表現できる4状態のうち3状態しか使用しない)である.また,入力IA=1, IB=0 の場合の次状態QA+, QB+および出力CA, CBはドントケア"−"とする.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
[B] [A]と同様に冗長2進表現した1桁数値を,今度は,ビットタイムごとに逐次的に(時間系列で順々に)入力して,時間系列で連続する2個の冗長2進表現数値の1桁どうしの半加算器(直列・逐次入力するので「直列半加算器」という)を最適化設計してみよう.この直列半加算器は,現状態Qを被加数,入力Iを加数として加算し,次状態Q+をその桁での和,出力Cを上位への桁上げとし,Q+I=Q+, C を表1の組み合わせ(表1での,XをQに,Y をIに,SをQ+にそれぞれ読み替える)にしたがって計算・状態遷移・出力する順序回路である.たとえば,[Q=I=1 ならば,Q+=0, C=1 (**)]である.また,この順序回路では,[A]と同様に,冗長2進表現の1桁数値で示せる状態"0"を"00","1"を"01","−1"を"11"のそれぞれ2ビットの論理値(2ビット,2個のフリップフロップ(FF)でこの順で"QA QB")で表現し,これらをそのままこの順序回路そのものの状態・出力(2ビット)とする.ただし,状態"10"は不使用でドントケアとする.たとえば,Q=−1 は,QA=1, QB=1 の2ビット(コード)で表現する.したがって,最適化設計する論理回路は,図2に示すように,IA, IBを入力,QA,QBを状態(出力も兼ねる),CA,CBを出力とし,2個のFFA, FFB(それぞれのFF状態(=FF出力)がQA,QB)を備える2入力4出力順序回路となる.ただし,QA=1, QB=0 はドントケア状態"−"であるから,論理設計する順序回路は不完全指定順序回路(2ビット状態(2個のFF)で表現できる4状態のうち3状態しか使用しない)である.また,入力IA=1, IB=0 の場合の次状態QA+, QB+および出力CA, CBはドントケア"−"とする.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)