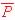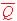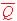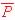「論理回路とその設計」 演習問題【11】
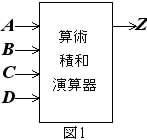 [A] 図1は2進数1ビット(桁)の<算術>積和演算器である.この演算器は,それぞれ1ビットの2進数値 A, B, C, D の4個を入力として,
[A] 図1は2進数1ビット(桁)の<算術>積和演算器である.この演算器は,それぞれ1ビットの2進数値 A, B, C, D の4個を入力として,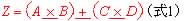 という算術積和演算を行い,1ビットの2進数値 Z を出力とする(桁上げは無視する).式1における算術演算子(記号)の機能は,表1,2の通り,普通の算術演算の乗算(multiply)と加算(add)である(それぞれ論理演算の論理積(AND)と論理和(OR)と紛れがないように,常用の演算子に下線を引いてある).2進数値1ビットは1ビットの論理値と見なせるので,この算術積和演算器は,A, B, C, D を入力,Z を出力,とする4入力1出力の組み合わせ回路である.この組み合わせ回路を最適化設計しよう.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
という算術積和演算を行い,1ビットの2進数値 Z を出力とする(桁上げは無視する).式1における算術演算子(記号)の機能は,表1,2の通り,普通の算術演算の乗算(multiply)と加算(add)である(それぞれ論理演算の論理積(AND)と論理和(OR)と紛れがないように,常用の演算子に下線を引いてある).2進数値1ビットは1ビットの論理値と見なせるので,この算術積和演算器は,A, B, C, D を入力,Z を出力,とする4入力1出力の組み合わせ回路である.この組み合わせ回路を最適化設計しよう.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
(1) 入力 A, B, C, D の組み合わせに対して,式1と表1,2を用いて,出力 Z を求め,解答欄の真理値表を完成しなさい.
(2) (1)の真理値表から出力 Z を下記の対応するカルノー図に写して,それを用いて出力 Z を2段論理最小化し,積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
(3) (2)で得た出力の最小積和形をファクタリングによって多段論理最小化し,その結果を任意形論理式で示しなさい.ファクタリングによる式変形過程はすべて解答として明記しなさい.最小形が複数あっても,いずれか1つを示せばよい.
(4) (2)と(3)の論理式それぞれに対応する論理<回路>どうしの最適化の度合い(程度)について,定量的に(数値を示して)比較・評価しなさい.
(5) 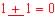 について,「
について,「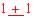 はドントケア(don't care)("−"と表す)」と見なして設計する組み合わせ回路の出力を Z ' とする. この出力 Z ' をカルノー図によって2段論理最小化し,積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
はドントケア(don't care)("−"と表す)」と見なして設計する組み合わせ回路の出力を Z ' とする. この出力 Z ' をカルノー図によって2段論理最小化し,積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
(6) 「算術演算と論理演算」あるいは「2進数値と論理値」の観点で,式1の算術(演算)式と(5)で示した論理(演算)式とを数学的に比較し,コメントしなさい.
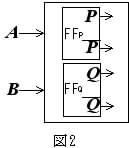 [B] 図2は,2ビットの入力 A, B と2ビットの(現)状態 P, Q を持つ2ビット入力-状態比較・変換器である.この入力-状態比較・変換器の機能は表3の状態遷移表(入力 A, B と次状態 P+, Q+との対応表)で示してある. この入力-状態比較・変換器を2個のフリップフロップ FFP と FFQ を持つ順序回路として最適化設計しよう.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
[B] 図2は,2ビットの入力 A, B と2ビットの(現)状態 P, Q を持つ2ビット入力-状態比較・変換器である.この入力-状態比較・変換器の機能は表3の状態遷移表(入力 A, B と次状態 P+, Q+との対応表)で示してある. この入力-状態比較・変換器を2個のフリップフロップ FFP と FFQ を持つ順序回路として最適化設計しよう.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
(1) 解答欄の状態遷移表について,表3
の状態遷移表にある現状態 P, Q を論理値に展開して次状態 P+, Q+ 列を埋め,完成しなさい.
(2) まず,この順序回路をT-FFによって構成する. (1)で作った状態遷移表に,解答欄に添付したT-FFの入力要求表を用いて,FFP と FFQ の入力要求である TP, TQ 列を連結して,拡大入力要求表(拡大状態遷移表)を作りなさい.
| 表3 |
| A |
B |
P+ |
Q+ |
(機能) |
| 0 |
0 |
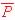 |
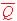 |
(トグル) |
| 0 |
1 |
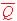 |
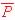 |
(トグル・交換) |
| 1 |
0 |
Q |
P |
(交換) |
| 1 |
1 |
P |
Q |
(不変) |
(3) (2)で作った拡大状態遷移表のTP, TQ 列を解答欄の対応するカルノー図に写し,それぞれを2段論理最小化して,FFP と FFQ の入力要求である TP, TQ の積和形論理式を求めなさい. カルノー図による操作はすべて解答として明記しなさい.
(4) (3)で得たTP, TQ の最小積和形のそれぞれをファクタリングによって多段論理最小化し,その結果を任意形論理式で示しなさい. ファクタリングによる式変形過程はすべて解答として明記しなさい. TP, TQ ともに,最小形が複数あっても,それぞれいずれか1つを示せばよい.
(5) 「ファクタリング」は論理関数(式)上での操作である.この「ファクタリング」は論理<回路>上ではどのような操作となるか,説明しなさい.
(6) 今度は,この順序回路をJK-FFによって構成する. (1)で作った状態遷移表に,解答欄に添付したJK-FFの入力要求表を用いて,FFP と FFQ の入力要求である JP, KP, JQ, KQ 列を連結して,拡大入力要求表(拡大状態遷移表)を作りなさい.
(7) (6)で作った拡大状態遷移表の JP, KP, JQ, KQ 列を解答欄の対応するカルノー図に写し,それぞれを2段論理最小化して,FFP と FFQ の入力要求である JP, KP, JQ, KQ の積和形論理式を求めなさい. カルノー図による操作はすべて解答として明記しなさい.
(8) (3)で設計したT-FFによる順序<回路>と(7)で設計したJK-FFによる順序<回路>の空間最適化の度合い(程度)について,使用FFの能力(機能)に言及して,定量的に(数値を示して)比較・コメントしなさい.
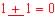 について,「
について,「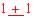 はドントケア(don't care)("−"と表す)」と見なして設計する組み合わせ回路の出力を Z ' とする. この出力 Z ' をカルノー図によって2段論理最小化し,積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
はドントケア(don't care)("−"と表す)」と見なして設計する組み合わせ回路の出力を Z ' とする. この出力 Z ' をカルノー図によって2段論理最小化し,積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい. [A] 図1は2進数1ビット(桁)の<算術>積和演算器である.この演算器は,それぞれ1ビットの2進数値 A, B, C, D の4個を入力として,
[A] 図1は2進数1ビット(桁)の<算術>積和演算器である.この演算器は,それぞれ1ビットの2進数値 A, B, C, D の4個を入力として,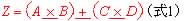 という算術積和演算を行い,1ビットの2進数値 Z を出力とする(桁上げは無視する).式1における算術演算子(記号)の機能は,表1,2の通り,普通の算術演算の乗算(multiply)と加算(add)である(それぞれ論理演算の論理積(AND)と論理和(OR)と紛れがないように,常用の演算子に下線を引いてある).2進数値1ビットは1ビットの論理値と見なせるので,この算術積和演算器は,A, B, C, D を入力,Z を出力,とする4入力1出力の組み合わせ回路である.この組み合わせ回路を最適化設計しよう.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
という算術積和演算を行い,1ビットの2進数値 Z を出力とする(桁上げは無視する).式1における算術演算子(記号)の機能は,表1,2の通り,普通の算術演算の乗算(multiply)と加算(add)である(それぞれ論理演算の論理積(AND)と論理和(OR)と紛れがないように,常用の演算子に下線を引いてある).2進数値1ビットは1ビットの論理値と見なせるので,この算術積和演算器は,A, B, C, D を入力,Z を出力,とする4入力1出力の組み合わせ回路である.この組み合わせ回路を最適化設計しよう.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
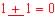 について,「
について,「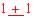 はドントケア(don't care)("−"と表す)」と見なして設計する組み合わせ回路の出力を Z ' とする. この出力 Z ' をカルノー図によって2段論理最小化し,積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
はドントケア(don't care)("−"と表す)」と見なして設計する組み合わせ回路の出力を Z ' とする. この出力 Z ' をカルノー図によって2段論理最小化し,積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい. [B] 図2は,2ビットの入力 A, B と2ビットの(現)状態 P, Q を持つ2ビット入力-状態比較・変換器である.この入力-状態比較・変換器の機能は表3の状態遷移表(入力 A, B と次状態 P+, Q+との対応表)で示してある. この入力-状態比較・変換器を2個のフリップフロップ FFP と FFQ を持つ順序回路として最適化設計しよう.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
[B] 図2は,2ビットの入力 A, B と2ビットの(現)状態 P, Q を持つ2ビット入力-状態比較・変換器である.この入力-状態比較・変換器の機能は表3の状態遷移表(入力 A, B と次状態 P+, Q+との対応表)で示してある. この入力-状態比較・変換器を2個のフリップフロップ FFP と FFQ を持つ順序回路として最適化設計しよう.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)