「論理回路とその設計」 演習問題【14】
[A] 基本論理演算と(論理関係を表す)日本語との対応は,NOT演算: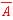 は「A でない」;AND演算:
は「A でない」;AND演算: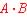 は「A かつ B」;OR演算:
は「A かつ B」;OR演算: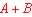 は「A または B」;である.次の <日本語で表した論理関係> を実現する組み合わせ回路を最適化設計してみよう.ただし,日本語でのカッコの優先順位は,〔「『( )』」〕と,最内側( )が最上位(最初に解決すべき論理関係)で,内から外へと順位が下がり,最外側〔 〕が最下位(最後に解決すべき論理関係)とする.以下の問は,論理式及びカルノー図による「論理表現」方法に関する比較考察を主としたものである.(1)〜(8)の問,及び,各問での途中経過をチェックする(i)(ii)…の小問,のそれぞれすべてに答えなさい.また,解答はこの解答用紙のすべて決められた個所で行いなさい.
は「A または B」;である.次の <日本語で表した論理関係> を実現する組み合わせ回路を最適化設計してみよう.ただし,日本語でのカッコの優先順位は,〔「『( )』」〕と,最内側( )が最上位(最初に解決すべき論理関係)で,内から外へと順位が下がり,最外側〔 〕が最下位(最後に解決すべき論理関係)とする.以下の問は,論理式及びカルノー図による「論理表現」方法に関する比較考察を主としたものである.(1)〜(8)の問,及び,各問での途中経過をチェックする(i)(ii)…の小問,のそれぞれすべてに答えなさい.また,解答はこの解答用紙のすべて決められた個所で行いなさい.
< 「W かつ Z」 または 〔(Z でない) かつ 「『(W でない) かつ (Y でない)』 または 『X かつ Y』」〕 >
(1) 次の(i)(ii)の順で,上記の日本語で表した論理関係を論理式(W,X,Y,Z の4論理変数)で表現しなさい.(i) この日本語を,論理変数,論理演算記号 ,及び,"(" ")" の重なり(ネスト)で表現する論理式にしなさい.ただし,公理「NOTの演算順位はANDやORよりも高い」に従って,日本語での(…でない)のカッコ( )に対応する論理式での "(" ")" は不要であり,(i)の解答では省きなさい.(ii) 公理「ANDの演算順位がORよりも高い」に従って,(i)の論理式から必要な "(" ")" 以外はすべて省き,(1)の解答としなさい.
,及び,"(" ")" の重なり(ネスト)で表現する論理式にしなさい.ただし,公理「NOTの演算順位はANDやORよりも高い」に従って,日本語での(…でない)のカッコ( )に対応する論理式での "(" ")" は不要であり,(i)の解答では省きなさい.(ii) 公理「ANDの演算順位がORよりも高い」に従って,(i)の論理式から必要な "(" ")" 以外はすべて省き,(1)の解答としなさい.
(2) (1)の論理式を積和形(AND項をORで結んだ2次元論理式)に変換しなさい.この操作は,「分配則による展開(「共通リテラルのくくり出し」であるファクタリングとは逆)操作による,(1)の論理式(3次元以上)で残っていた "(" ")" の取り外し」という, 簡単な式変形である.
(3) (2)の積和形論理式を標準積和形に変換しなさい.ただし,「積和形論理式表現と1対1対応するカルノー図表現が存在する」に従って,「真理値表を作成せずに,カルノー図表現のみによる次の(i)〜(iii)の操作によって得る解答」を原則(満点)とする.(i) (2)で得た積和形論理式をカルノー図で表現しなさい.(ii) (i)で得たカルノー図のすべての○を取り外し,バラバラの1個セル(ここで「セル」とは「"1"セル」であり,以下単に「セル」という)だけのカルノー図にしなさい.ただし,各1個セルを囲む○は省略しなさい.(iii) (ii)のカルノー図でバラした1個セルそれぞれを最小項(W,X,Y,Z のリテラルすべてが現れるAND項)として読み取りなさい. (iii)の最小項をORで結んだ2次元論理式が(3)の解答の標準積和形である.(ここで,この(3)の(ii)の○なしカルノー図を,(4)以降で使う解答用紙のカルノー図すべてに,コピーしておきなさい.)
(4) (3)の標準積和形をもとにして,「カルノー図による操作」によって2段論理最小化し(問(4)〜(6)の順で行う),最小積和形を求めてみよう.
まず,(3)の標準積和形に対応するカルノー図((3)の(ii))をもとにして,それに次の操作(i)〜(iv)を順に適用することによって,主項(積和形を構成するAND項のうちで他のどのAND項にも包含されないAND項)をすべて求めなさい.(i) 孤立1個セル(隣接2個セルに併合できない1個セル)を○で囲みなさい.(ii) 孤立2個セル(隣接4個セルに併合できない2個セル)を○で囲みなさい.(iii) 孤立4個セル(隣接8個セルに併合できない4個セル)を○で囲みなさい.(iv) (i)〜(iii)で得た○をすべて重畳したカルノー図を示しなさい. (i)〜(iii)あるいは(iv)のカルノー図の○をAND項として読み取って,すべての主項を求めなさい.ただし,(i)〜(iii)の操作では,孤立セルが存在せずに○が付かない場合もある.
(5) 次の(i)(ii)の操作によって,(4)の主項の中から,必須主項を見つけなさい. (i) (4)の主項による積和形を表現するカルノー図((4)の(iv))をチェックして,特異最小項(唯一主項だけが包含する最小項)に対応する1個セル(唯一○だけが囲む1個セル)を,(4)の(iv)のカルノー図上で斜線による網がけでマーキングしなさい.(ii) (i)の特異最小項を囲む○をカルノー図上で示しなさい. (ii)の○で示す主項が必須主項である.
(6) (5)の(ii)をコピーしたカルノー図上で,(5)の必須主項に対応する○((5)の(ii))だけでは囲めていない1個セルすべてを最小個数の○で囲みなさい.この○が選択すべき主項である.これですべての1個セルが最小個数の○で囲めたはずである.この○を主項(AND項)として読み取り,ORで結んで,最小積和形として示しなさい.
(7) (6)の最小積和形論理式にファクタリング(「共通リテラルのくくり出し」による式変形)を適用し,多段論理最小化した論理式を求めなさい.
(8) (7)の多段論理最小化した論理式に対応する論理回路(回路図)を,次の(i)(ii)に従って,示しなさい.(i) (7)の論理式をテクノロジマッピングによって,対応するAND/OR回路にしなさい.(ii) (i)を回路変換によってNAND回路にしなさい.
[B] 上階⇔中階⇔下階を昇降するエレベータを「U」(Up)と「D」(Down)の2つのボタンで制御する.その「コントローラ」を2個のDフリップフロップ( FFP, FFQ とし,その状態をそれぞれ P, Q ,入力をそれぞれ DP, DQ とする)による同期式順序回路として設計してみよう.このコントローラの状態は「上」「中」「下」の3つであり,エレベータが現在位置する上中下階のいずれかをこの順で表している.また,「U」「D」2つのボタン(オフ/オンはこの順で論理値 "0" / "1" に対応)によって,表1
| 表1 |
| U |
D |
動作(記号) |
現階での実動作 |
| 0 |
0 |
(停)止 |
上中下階とも止 |
| 0 |
1 |
(下)降 |
上中階でのみ降 (下階では止) |
| 1 |
0 |
(上)昇 |
中下階でのみ昇 (上階では止) |
| 1 |
1 |
(作)動 |
上階で降,下階で昇 (中階で止) |
に示す通り,エレベータの「止」「降」「昇」「動」の4つの実動作を指定する.すなわち,このコントローラは,日本語による記号表現で,「『 止 / 降 / 昇 / 動 』の4種類の入力によって,『 上 / 中 / 下 』の3状態間を状態遷移する」同期式順序回路である.ただし,同期式順序回路であるので,入力と状態遷移はクロックによってビットタイムごとに同期する.次の問すべてに答えなさい.解答はこの解答用紙の決められた個所で行いなさい.
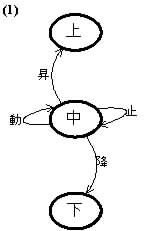
(1) 日本語による記号表現によって,状態遷移図を書きなさい.すなわち,この状態遷移図においては,状態は「 上 / 中 / 下 」(各節点名),入力は「 止 / 降 / 昇 / 動 」(状態遷移を示す矢印上に付記)である.入力は4種類なので,各状態(節点)から出る状態遷移(矢印)は4本である.ただし,一部は例として記入済である.
(2) (1)の状態遷移図を,日本語による記号表現の状態遷移表にしなさい.この状態遷移表では,縦軸が「現状態」,横軸が「入力」,両軸が交差する各欄が「次状態」である. ただし,一部((1)での記入済み例の部分)は例として記入済である.
(3) 次に,日本語による記号表現を論理値に割り当てる.入力「 止 / 降 / 昇 / 動 」は,既に表1に示したように,この順で,UD = "00"(止), "01"(降), "10"(昇), "11"(動) と決めてある.状態「 中 / 下 / 上(順に注意)」については,この順(順に注意)で,PQ = "00"(中), "01"(下), "10"(上) と割り当てる.PQ ="11" は割り当てなし(ドントケア)である.これらの入力論理値及び状態割り当てに従って,(2)の日本語表現による状態遷移表の各欄の下段に,対応する論理値を記入して,論理値による状態遷移表を完成しなさい.
(4) (3)の状態遷移表(論理値による部分)によって,拡大状態遷移表の P+ と Q+ の各列を埋めて,完成しなさい.
(5) このコントローラをD-FF (FFP, FFQ) によって構成する.右記のD-FFの入力要求表に従うと,(4)の拡大状態遷移表から作る拡大入力要求表での DP, DQ 列は拡大状態遷移表の P+, Q+ 列それぞれと同じである.この拡大入力要求表をカルノー図に写し, DP, DQ の各最小積和形論理式を求めなさい.
(6) 状態割り当てを変更すると,各FFの入力条件式の最小積和形やその最適化の度合い(最小積和形論理式におけるリテラル総数)も異なってくる.具体的に,この順序回路の設計において,状態「中」を PQ = "00" ではなくて,PQ ="11" に割り当てると,DP, DQ の最適化の度合いはどうなるか(良くなるか悪くなるか),また,なぜそう推定できるのか,定性的に説明しなさい.(入力条件式やその最小積和形を求めることは不要である.)
| (2) (3)
次状態 P+Q+ |
入力 UD |
| 0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
| 止 |
降 |
昇 |
動 |
| 現状態 PQ |
中 |
中 |
下 |
上 |
中 |
| 0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
| 下 |
|
|
|
|
| 0 |
1 |
|
|
|
|
|
|
|
|
| 上 |
|
|
|
|
| 1 |
0 |
|
|
|
|
|
|
|
|
 ,及び,"(" ")" の重なり(ネスト)で表現する論理式にしなさい.ただし,公理「NOTの演算順位はANDやORよりも高い」に従って,日本語での(…でない)のカッコ( )に対応する論理式での "(" ")" は不要であり,(i)の解答では省きなさい.(ii) 公理「ANDの演算順位がORよりも高い」に従って,(i)の論理式から必要な "(" ")" 以外はすべて省き,(1)の解答としなさい.
,及び,"(" ")" の重なり(ネスト)で表現する論理式にしなさい.ただし,公理「NOTの演算順位はANDやORよりも高い」に従って,日本語での(…でない)のカッコ( )に対応する論理式での "(" ")" は不要であり,(i)の解答では省きなさい.(ii) 公理「ANDの演算順位がORよりも高い」に従って,(i)の論理式から必要な "(" ")" 以外はすべて省き,(1)の解答としなさい.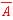 は「A でない」;AND演算:
は「A でない」;AND演算: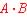 は「A かつ B」;OR演算:
は「A かつ B」;OR演算: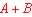 は「A または B」;である.次の <日本語で表した論理関係> を実現する組み合わせ回路を最適化設計してみよう.ただし,日本語でのカッコの優先順位は,〔「『( )』」〕と,最内側( )が最上位(最初に解決すべき論理関係)で,内から外へと順位が下がり,最外側〔 〕が最下位(最後に解決すべき論理関係)とする.以下の問は,論理式及びカルノー図による「論理表現」方法に関する比較考察を主としたものである.(1)〜(8)の問,及び,各問での途中経過をチェックする(i)(ii)…の小問,のそれぞれすべてに答えなさい.また,解答はこの解答用紙のすべて決められた個所で行いなさい.
は「A または B」;である.次の <日本語で表した論理関係> を実現する組み合わせ回路を最適化設計してみよう.ただし,日本語でのカッコの優先順位は,〔「『( )』」〕と,最内側( )が最上位(最初に解決すべき論理関係)で,内から外へと順位が下がり,最外側〔 〕が最下位(最後に解決すべき論理関係)とする.以下の問は,論理式及びカルノー図による「論理表現」方法に関する比較考察を主としたものである.(1)〜(8)の問,及び,各問での途中経過をチェックする(i)(ii)…の小問,のそれぞれすべてに答えなさい.また,解答はこの解答用紙のすべて決められた個所で行いなさい.
 ,及び,"(" ")" の重なり(ネスト)で表現する論理式にしなさい.ただし,公理「NOTの演算順位はANDやORよりも高い」に従って,日本語での(…でない)のカッコ( )に対応する論理式での "(" ")" は不要であり,(i)の解答では省きなさい.(ii) 公理「ANDの演算順位がORよりも高い」に従って,(i)の論理式から必要な "(" ")" 以外はすべて省き,(1)の解答としなさい.
,及び,"(" ")" の重なり(ネスト)で表現する論理式にしなさい.ただし,公理「NOTの演算順位はANDやORよりも高い」に従って,日本語での(…でない)のカッコ( )に対応する論理式での "(" ")" は不要であり,(i)の解答では省きなさい.(ii) 公理「ANDの演算順位がORよりも高い」に従って,(i)の論理式から必要な "(" ")" 以外はすべて省き,(1)の解答としなさい.