「論理回路とその設計」 演習問題【15】
[A] 2ビット2進数の(算術)乗算器と除算器を組み合わせ回路として最適化設計してみよう. 乗算器と除算器のどちらも,入力は,2ビット2進数である被演算数(被乗数または被除数)の A1 A0 および演算数(乗数または除数)の B1 B0 である. 出力は,乗算器からは4ビット2進数の積 M3 M2 M1 M0 ,除算器からは2ビット2進数の商 Q1 Q0 および剰余(余り)R1 R0 ,のそれぞれである.したがって,乗算器は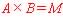 の機能を持つ4入力(A1,A0,B1,B0) 4出力(M3,M2,M1,M0)の,除算器は
の機能を持つ4入力(A1,A0,B1,B0) 4出力(M3,M2,M1,M0)の,除算器は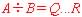 の機能を持つ4入力(A1,A0,B1,B0) 4出力(Q1,Q0,R1,R0)の,それぞれ組み合わせ回路である. ただし,除算器において,除数B(入力 B1 B0)が"0"の除算は(数学的に)不能であるので,その場合の商Q(出力 Q1 Q0)と剰余R(出力 R1 R0)はドントケア"−"とする.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可. )
の機能を持つ4入力(A1,A0,B1,B0) 4出力(Q1,Q0,R1,R0)の,それぞれ組み合わせ回路である. ただし,除算器において,除数B(入力 B1 B0)が"0"の除算は(数学的に)不能であるので,その場合の商Q(出力 Q1 Q0)と剰余R(出力 R1 R0)はドントケア"−"とする.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可. )
| A |
B |
M |
Q |
R |
| 0 |
0 |
0 |
− |
− |
| 0 |
1 |
0 |
0 |
0 |
| 0 |
2 |
0 |
0 |
0 |
| 0 |
3 |
0 |
0 |
0 |
| 1 |
0 |
0 |
− |
− |
| 1 |
1 |
1 |
1 |
0 |
| 1 |
2 |
2 |
0 |
1 |
| 1 |
3 |
3 |
0 |
1 |
| 2 |
0 |
0 |
− |
− |
| 2 |
1 |
2 |
2 |
0 |
| 2 |
2 |
4 |
1 |
0 |
| 2 |
3 |
6 |
0 |
2 |
| 3 |
0 |
0 |
− |
− |
| 3 |
1 |
3 |
3 |
0 |
| 3 |
2 |
6 |
1 |
1 |
| 3 |
3 |
9 |
1 |
0 |
(1) 右記の表(実際には解答欄にあり,ここでは一部列のみを掲載)には,10進数値での入力(AとB)および2進数値での入力( A1,A0 と B1,B0 )に対する10進数値での出力(MおよびQとR)を既に記入済(解答欄では,網掛け列)である.10進数値での出力(MおよびQとR)を2進数値での出力(M3,M2,M1,M0およびQ1,Q0とR1,R0)に変換して空欄を埋めて,真理値表として完成しなさい.
(2) まず,(1)の真理値表から乗算器の出力M3,M2,M1,M0のそれぞれを解答欄の対応するカルノー図に写して,それを用いて出力M3,M2,M1,M0のそれぞれを2段論理最小化し,最小積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
(3) (2)で求めた出力M3,M2,M1,M0の各最小積和形のうちで,ファクタリングを用いて多段論理最小化できるものがあれば,それらすべて(の結果)を論理式で示しなさい.
(4) 次に,(1)の真理値表から除算器の出力Q1,Q0,R1,R0のそれぞれを解答欄の対応するカルノー図に写して,それを用いて出力Q1,Q0,R1,R0のそれぞれを2段論理最小化し,最小積和形論理式で示しなさい.カルノー図による操作はすべて解答として明記しなさい.
(5) (4)で求めた出力Q1,Q0,R1,R0の各最小積和形のうちで,ファクタリングを用いて多段論理最小化できるものがあれば,それらすべて(の結果)を論理式で示しなさい.
(6) (2)の2段論理最小化した4入力4出力乗算器と(4)の2段論理最小化した4入力4出力除算器とは,入力が共通であるので,両者を4入力8出力の組み合わせ回路(乗除算器)にまとめる(併合する)ことができる.その際,共有(共用)ゲートの存在によって,「2段」という時間最適化を保持したまま†,さらなる空間最適化ができるかどうかについて,(2)や(4)の解答である最小積和形論理式を引用する,および,(2)や(4)の解答のために作成したカルノー図を用いる,の2点(どちらも解答は必須)によって説明しなさい.ただし,「『2段』という時間最適化を保持したまま†」とは,「ANDゲート(論理積項に対応)もORゲート(論理和項に対応)も,共有ゲートも含めて,多入力ゲート(多項演算項に対応)が使用できる場合は,それを優先して使用する(多入力ゲートを2入力ゲートに展開しない)」こととする.
(7) (6)と同様に,今度は,(3)のファクタリングした後の4入力4出力乗算器と(5)のファクタリングした後の4入力4出力除算器とを併せて4入力8出力の組み合わせ回路にまとめた場合,共有(共用)ゲートの存在によって,さらなる空間最適化ができるかどうかについて,(2)(3)や(4)(5)の解答である論理式を引用することによって説明しなさい.
[B] 3ビットの2進/グレイコードカウンタを3個のフリップフロップ(FF-P, FF-Q, FF-Rとし,その状態をそれぞれ P, Q, R とする)を用いる同期式順序回路として設計してみよう.3ビットの 2進/グレイコードカウンタとは,2進カウンタ動作とグレイコードカウンタ動作との切り替え制御用に1入力 S を持ち,[ S=0のときは,PQR = 000 → 001 → 010 → 011 → 100 → 101 → 110 → 111 → 000 → …(以下繰り返しのため省略) ]という2進カウンタ動作を,[ S=1のときは,PQR = 000 → 001 → 011 → 010 → 110 → 111 → 101 → 100 → 000 → …(以下繰り返しのため省略) ]というグレイコードカウンタ動作を,それぞれ行う.同期式順序回路であるので,入力と状態遷移はクロックによって同期することを前提とするが,解答では,クロックは無視・省略しなさい.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
(1) カウンタの設計では,一般的な順序回路の設計手順の一番最初に行う「状態割り当て」は不要である.「状態割り当てとは何か」を明らかにすることによって,「カウンタの設計では,状態割り当ては不要である」理由について説明しなさい.
(2) この設計では,状態遷移図を作成しなくても,上記の[動作説明文]によって示す状態遷移である PQR → P+Q+R+ それぞれを表に書き写すことによって,拡大状態遷移表を作成できる. 解答欄の拡大状態遷移表の次状態 P+ 列,Q+ 列,R+ 列を埋めて完成しなさい.
(3) まず,この順序回路を3個のD-FFによって構成する.D-FFの入力要求表は右記した通りであり,D-FFの場合には,(2)で作った拡大状態遷移表の P+,Q+,R+ 列がそのままそれぞれ DP,DQ,DR 列となることに注意して,この拡大状態遷移表の DP,DQ,DR 列を解答欄の対応するカルノー図に写し,入力条件式 DP, DQ, DR のそれぞれを2段論理最小化し,最小積和形論理式で示しなさい. カルノー図による操作はすべて解答として明記しなさい.
(4) (3)で求めた DP, DQ, DR の各最小積和形のうちで,ファクタリングを用いて多段論理最小化できるものがあれば,それらすべて(の結果)を論理式で示しなさい.
(5) 次に,この順序回路を3個のJK-FFによって構成する.JK-FFの入力要求表は右記した通りであり,これを用いて,(2)で作った拡大状態遷移表の右側のJP,KP,JQ,KQ,JR,KR 列を埋めて拡大入力要求表として完成しなさい.この拡大入力要求表の JP,KP,JQ,KQ,JR,KR 列を解答欄の対応するカルノー図に写し,入力条件式 JP ,KP ,JQ ,KQ ,JR ,KR のそれぞれを2段論理最小化し,最小積和形論理式で示しなさい. カルノー図による操作はすべて解答として明記しなさい.
(6) (5)で求めた2段論理最小化した入力条件式 JP ,KP ,JQ ,KQ ,JR ,KR で構成する順序回路全体において,共有(共用)ゲートの存在によって,「2段」という各FF入力での時間最適化を保持したまま†,さらなる空間最適化ができるかどうかについて,(5)の解答である最小積和形論理式を引用する,および,(5)の解答のために作成したカルノー図を用いる,の2点(どちらも解答は必須)によって説明しなさい.ただし,「『2段』という時間最適化を保持したまま†」とは,「ANDゲート(論理積項に対応)もORゲート(論理和項に対応)も,共有ゲートも含めて,多入力ゲート(多項演算項に対応)が使用できる場合は,それを優先して使用する(多入力ゲートを2入力ゲートに展開しない)」こととする.
(7) (5)で求めた JP ,KP ,JQ ,KQ ,JR ,KR の各最小積和形のうちで,ファクタリングを用いて多段論理最小化できるものがあれば,それらすべて(の結果)を論理式で示しなさい.
(8) (3)と(5)で最適化(2段論理最小化)設計した順序回路(2進/グレイコードカウンタ)それぞれの(3個のFFの空間サイズを除く)全体の空間サイズを定量的に(2入力AND/ORゲート総数によって)求めて,(3)で使用したD-FFと(5)で使用したJK-FFの機能(能力)について比較・コメントしなさい.
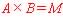 の機能を持つ4入力(A1,A0,B1,B0) 4出力(M3,M2,M1,M0)の,除算器は
の機能を持つ4入力(A1,A0,B1,B0) 4出力(M3,M2,M1,M0)の,除算器は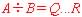 の機能を持つ4入力(A1,A0,B1,B0) 4出力(Q1,Q0,R1,R0)の,それぞれ組み合わせ回路である. ただし,除算器において,除数B(入力 B1 B0)が"0"の除算は(数学的に)不能であるので,その場合の商Q(出力 Q1 Q0)と剰余R(出力 R1 R0)はドントケア"−"とする.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可. )
の機能を持つ4入力(A1,A0,B1,B0) 4出力(Q1,Q0,R1,R0)の,それぞれ組み合わせ回路である. ただし,除算器において,除数B(入力 B1 B0)が"0"の除算は(数学的に)不能であるので,その場合の商Q(出力 Q1 Q0)と剰余R(出力 R1 R0)はドントケア"−"とする.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可. )