「論理回路とその設計」 演習問題【16】
[A] 基本論理演算と(論理関係を表す)日本語との対応は,NOT演算 はX でない」;AND演算 X ・Y は「X かつY 」,「X もY もどちらも(両方とも)」;OR演算 X+Y は「X またはY 」,「X かY のどちらか(片方でも)」;などである.「システムの故障診断器」を組み合わせ回路として設計する.この故障診断器では,「故障している(以降では,単に「故障」と書く)」を論理値"1",「故障していない(「
はX でない」;AND演算 X ・Y は「X かつY 」,「X もY もどちらも(両方とも)」;OR演算 X+Y は「X またはY 」,「X かY のどちらか(片方でも)」;などである.「システムの故障診断器」を組み合わせ回路として設計する.この故障診断器では,「故障している(以降では,単に「故障」と書く)」を論理値"1",「故障していない(「 」と書く)」を論理値"0"とする.「故障診断」は「(論理としての)故障("1")か
」と書く)」を論理値"0"とする.「故障診断」は「(論理としての)故障("1")か ("0")かを調べるあるいは決める(判定する)こと」である.
("0")かを調べるあるいは決める(判定する)こと」である.
4点の部品:A, B, C, D を組み合わせて構成するシステム S がある. 「システム S が故障(S=1, =0)か
=0)か (S=0,
(S=0,  =1)か」は部品:A, B, C, D それぞれの故障診断結果(論理値)を次の故障診断テンプレートに当てはめて診断できるものとする.
=1)か」は部品:A, B, C, D それぞれの故障診断結果(論理値)を次の故障診断テンプレートに当てはめて診断できるものとする.
●S が故障(S=1)は,次の1.または2.のどちらか(OR)の場合.(それ以外は, (S=0).)
(S=0).)
1. A が (A=0あるいは単に
(A=0あるいは単に ),かつ(AND),次の(1)(2)のどちらか(OR)の場合.
),かつ(AND),次の(1)(2)のどちらか(OR)の場合.
2. A が故障(A=1あるいは単に A),かつ(AND),次の(1)(2)のどちらか(OR)の場合.
この日本語で表した故障診断テンプレートに従って S を4変数 A,B,C,D の論理式で表現し,これをもとに,「(4点の部品:A, B, C, D それぞれの故障診断結果によるシステム S 全体の)故障診断器」を4入力(A,B,C,D)1出力(S)の組み合わせ回路として最適化設計する.次の問すべてに答えなさい. (解答の論理式では,AND記号"・"は省略しなさい.)
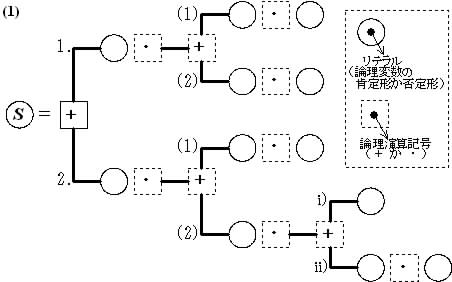
(1) この故障診断テンプレートを解答欄にある論理式(表現)作成用マップ(論理演算記号は既に記入済み)に写し(○内にリテラルを記入し)なさい.この論理式作成用マップを使用して,故障診断テンプレートと1対1対応する S の論理を論理式(A,B,C,D の4論理変数)で表現しなさい.
(2) (1)の論理式を積和形論理式(AND項をORで結んだ2次元論理式)に変換しなさい.この変換操作は,「分配則(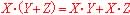 )による展開操作による簡単な式変形である.
)による展開操作による簡単な式変形である.
(3) 「積和形論理式表現と1対1対応するカルノー図表現が存在する」に従って,(2)の積和形論理式をカルノー図(AND項に対応する1個セルまたは2個セルは○で囲んで明示しなさい)で表現しなさい.
(4) (3)のカルノー図上の1個セルそれぞれを(バラして)最小項(A,B,C,D のリテラルすべてが現れるAND項)として読み取り,それらをORで結ぶことによって,(2)の積和形論理式を標準積和形に変換しなさい.
(5) (4)の標準積和形に対応する(バラした○なし1個セルで構成する)カルノー図((3)のカルノー図の○以外を解答欄にコピーしたものを出発点にして使用しなさい)によって2段論理最小化を行い,最小積和形を求めなさい.最小積和形が複数ある場合はそのすべてを求めなさい. カルノー図による操作はすべて解答として明記しなさい.
(6) (5)の最小積和形論理式(すべて)において,ファクタリングによって多段論理最小化できるものがあれば,その結果を論理式として示しなさい.
(7) (6)のファクタリング操作をカルノー図で補助する方法について,(5)での操作後のカルノー図を例にとって,考察しなさい.
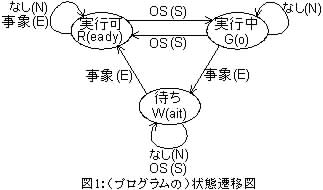
[B] OSは,「プログラムの実行管理」を,(a) (プログラムの)「状態」は「待ち(W(ait))」;「実行可(R(eady))」;「実行中(G(o))」;の3状態のどれかである;(b) (プログラムの)「状態遷移」は「無操作(N(one))」;「事象(発生)(E(vent))」;「OS(による)指令((O)S)」;のどれかによって生じる;(c) (プログラムの)「状態遷移」は図1の 状態遷移図に従う;によって行う.例えば,「待ち(W)」状態のときには,「事象(E)」によって「実行可(R)」状態へ遷移し,それ以外の「無操作(N)」や「OS指令(S)」では「待ち(W)」状態に留まる.普通はOS(ソフトウェア)が行っているこの「プログラムの実行管理」機能を,ここではハードウェア機構として実現してみよう.この「プログラム実行管理機構」は,図2のように,2個のフリップフロップ(FF-P, FF-Qとし,その状態をそれぞれ P, Q とする)及び2本の入力(OS指令:S,事象:E とする)を備える2ビット2入力同期式順序回路である.状態割り当てとして,「実行可(R)」を PQ = 01 ( P=0, Q=1,以下同様);「実行中(G)」を PQ = 11;「待ち(W)」を PQ = 00;PQ = 10 をドントケア(−);とする.また,入力 SE については,SE = 00 で「なし(無操作)(N)」;SE = 01 で「事象(E)」;SE = 10 で「OS指令(S)」;SE = 11 はドントケア(−);を示す.同期式順序回路であるので,入力と状態遷移はクロックによって同期するが,解答では,クロックの存在は省略しなさい.次の問すべてに答えなさい.(論理積(AND)記号"・"は省略可.)
(1) 図1の状態遷移図を状態 PQ と入力 SE の論理値("0"か"1")で書き直して,設計する同期式順序回路の状態遷移図(解答欄)としなさい.
(2) (1)の状態遷移図によって,拡大状態遷移表を作成しなさい.解答は,解答欄の拡大状態遷移表の次状態 P+ 列,Q+ 列を埋めることで行いなさい.
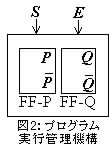
(3) まず,この順序回路を2個のD-FFによって構成する.D-FFの入力要求表は右記した通り( D = Q+ )であり,(2)で作った拡大状態遷移表の P+, Q+ 列がそのままそれぞれ DP, DQ 列となることに注意して,この拡大状態遷移表の DP, DQ 列を解答欄の対応するカルノー図に写し,入力条件式 DP, DQ のそれぞれを2段論理最小化し,最小積和形論理式で示しなさい. カルノー図による操作はすべて解答として明記しなさい.
(4) 次に,この順序回路を2個のT-FFによって構成する.T-FFの入力要求表は右上記した通りであり,これを用いて,(2)で作った拡大状態遷移表の右側の TP, TQ 列を埋めて拡大入力要求表として完成しなさい.この拡大入力要求表の TP, TQ 列を解答欄の対応するカルノー図に写し,入力条件式 TP, TQ のそれぞれを2段論理最小化し,最小積和形論理式で示しなさい. カルノー図による操作はすべて解答として明記しなさい.
(5) (4)で求めた2段論理最小化した入力条件式 TP, TQ で構成する順序回路全体において,共有(共用)ゲートの存在によって,「2段」という各FF入力での時間最適化を保持したまま†,さらなる空間最適化ができるかどうかについて,(4)の解答である最小積和形論理式を引用する,及び,(4)の解答のために作成したカルノー図を用いる,の2点(どちらも解答は必須)によって説明しなさい.ただし,「『2段』という時間最適化を保持したまま†」とは,「ANDゲート(論理積項に対応)もORゲート(論理和項に対応)も,共有ゲートも含めて,多入力ゲート(多項演算項に対応)が使用できる場合は,それを優先して使用する(多入力ゲートを2入力ゲートに展開しない)」こととする.
(6) (4)で求めた TP, TQ の各最小積和形のうちで,ファクタリングを用いて多段論理最小化できるものがあれば,それらすべて(の結果)を論理式で示しなさい.
(7) (5)と(6)について,「空間最適化の度合いの定量的な比較」及び「それらの最適化が両立する(同時に適用可能)か」についてコメントしなさい.
 (A=0あるいは単に
(A=0あるいは単に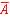 ),かつ(AND),次の(1)(2)のどちらか(OR)の場合.
),かつ(AND),次の(1)(2)のどちらか(OR)の場合.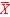 はX でない」;AND演算 X ・Y は「X かつY 」,「X もY もどちらも(両方とも)」;OR演算 X+Y は「X またはY 」,「X かY のどちらか(片方でも)」;などである.「システムの故障診断器」を組み合わせ回路として設計する.この故障診断器では,「故障している(以降では,単に「故障」と書く)」を論理値"1",「故障していない(「
はX でない」;AND演算 X ・Y は「X かつY 」,「X もY もどちらも(両方とも)」;OR演算 X+Y は「X またはY 」,「X かY のどちらか(片方でも)」;などである.「システムの故障診断器」を組み合わせ回路として設計する.この故障診断器では,「故障している(以降では,単に「故障」と書く)」を論理値"1",「故障していない(「 」と書く)」を論理値"0"とする.「故障診断」は「(論理としての)故障("1")か
」と書く)」を論理値"0"とする.「故障診断」は「(論理としての)故障("1")か ("0")かを調べるあるいは決める(判定する)こと」である.
("0")かを調べるあるいは決める(判定する)こと」である.
 =0)か
=0)か (S=0,
(S=0,  =1)か」は部品:A, B, C, D それぞれの故障診断結果(論理値)を次の故障診断テンプレートに当てはめて診断できるものとする.
=1)か」は部品:A, B, C, D それぞれの故障診断結果(論理値)を次の故障診断テンプレートに当てはめて診断できるものとする.
 (S=0).)
(S=0).)
 (A=0あるいは単に
(A=0あるいは単に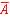 ),かつ(AND),次の(1)(2)のどちらか(OR)の場合.
),かつ(AND),次の(1)(2)のどちらか(OR)の場合. (B=0あるいは単に
(B=0あるいは単に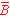 ),かつ(AND),C が故障(C=1あるいは単に C).
),かつ(AND),C が故障(C=1あるいは単に C).
 (C=0あるいは単に
(C=0あるいは単に ).
). (C=0あるいは単に
(C=0あるいは単に ).
).
 (B=0あるいは単に
(B=0あるいは単に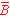 ),かつ(AND),次の i) ii)のどちらか(OR)の場合.
),かつ(AND),次の i) ii)のどちらか(OR)の場合. (C=0あるいは単に
(C=0あるいは単に ),かつ(AND),D が
),かつ(AND),D が (D=0あるいは単に
(D=0あるいは単に ).
).
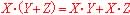 )による展開操作による簡単な式変形である.
)による展開操作による簡単な式変形である.
