（ f_n は「可"1"をカウント(計数)する，あるいは，可"1"だけに関わる」論理関数であるから，f_n に関する解答としての論理式はいずれも肯定形リテラルのみで表せて，それらの論理式には否定形リテラルは出現しないはずである．（ヒント2；ただし，問題文中及び試験時には不明示） ）

(1) (i) 下記の真理値表の f_n (n＝1,2,3,4) 列(4列)を埋めなさい．(ii) その真理値表から各出力 f_n (n＝1,2,3,4) を解答欄のカルノー図に写し，それを用いて各出力 f_n (n＝1,2,3,4) を2段論理最小化し，最小積和形論理式で示しなさい．カルノー図による操作はすべて解答として明記しなさい．

(2) (1)(ii)の f₂ と f₃ について，ファクタリングによって多段論理最小化し，それらすべて(の結果)を最小形論理式で示しなさい．上記の注^†に注意すると，「 f₂ と f₃ ともに，最小形は複数ある」と推定できる． f₂ と f₃ ともに，それらすべてを示しなさい．

(3) (2)で求めた(ファクタリング後の) f₂ と f₃ の2出力回路における「共用(共有)ゲートの有無」について，(2)の解答を引用して，簡潔に述べなさい．

(4) f₂^d と f₃^d を求めてみよう．(i) 上記の定義^‡(a)を適用( f₂, f₃ ともに論理式内に論理定数はないので(b)は適用の余地がない)することによって，f₂^d と f₃^d を和積形論理式として示しなさい． (ii) (i)で得られた和積形論理式の論理変数 A,B,C,D に論理定数"1"または"0"を代入することによって f₂^d と f₃^d の論理関数値を求め，下記の真理値表の f₂^d と f₃^d 列(2列)を埋めなさい．(iii) その真理値表から出力 f₂^d と f₃^d を解答欄のカルノー図に写し，それを用いて出力 f₂^d と f₃^d を2段論理最小化し，最小積和形論理式で示しなさい．カルノー図による操作はすべて解答として明記しなさい．(iv) f₂, f₂^d, f₃, f₃^d 相互間にあるすべての論理関係を論理式で表しなさい．(v) f₂ と f₃ との論理関係を日本語で述べなさい．

(5) 「f ^d が f の双対関数であることの証明」あるいは「 f から f ^d を求める方法」について，上記の定義^‡(b)だけ((a)は不使用)を適用して行う方法がある．すなわち，( f の)真理値表あるいはカルノー図だけで(だけをもとにして)行う方法である．これらの方法について，f₂ あるいは f₃ ((4)の解答過程における真理値表やカルノー図)を例にとって，簡潔に(真理値表やカルノー図は描かずに)説明しなさい．

(6) 投票者を m (m≧2) 人として，しきい値関数 f_n を一般化すると，f_n (n＝1,2,…,m) となる．(1)〜(5)は m＝4(偶数)の場合で，f₁＝f₄^d ( f₄＝f₁^d ) 及び「(4)(iv)の解(論理式)」である．また，m＝2(偶数)の場合，f₁＝f₂^d ( f₂＝f₁^d ) である(確かめなさい)．これらを参考にして，(i) m＝3(奇数)の場合，f₁＝f₃^d ( f₃＝f₁^d )，f₂＝f₂^d ( f₂ は自己双対関数)であることを示しなさい(証明しなさい)．次に，(ii) m＝2,3,4 の場合をもとに，m＝5(奇数)の場合に，f₁, f₂, f₃, f₄, f₅ 相互間にある双対関係について数学的に推定し，m＝2,3,4 と同様に，論理式で示しなさい(証明は不要である)．

[B] 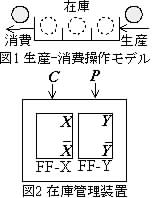図1は，ある製品に対して，(a) 「在庫」は3個まで(0,1,2,3個のいずれか)保管可能；(b) 「生産」は在庫を＋1個する(1個増やす)操作；(c) 「消費」は在庫を−1個する(1個減らす)操作；を管理する「生産-消費操作モデル」である． ただし，(a)の制約の下で，在庫が3個の状態では，(b)の生産操作は無操作(在庫の増はなく3個を保持)となり，在庫が0個の状態では，(c)の消費操作は無操作(在庫の減はなく0個を保持)となる．この生産-消費操作モデルを，図2で示すような，「在庫管理装置」，すなわち，「2入力 C, P 及び2個(FF-X, FF-Y)の状態保持用フリップフロップ(FF)(FF-X,Yの状態及び出力は X, Y )を備え，ビットタイムごとに入力 C, P とFF状態(出力) X, Y を論理値("0"か"1")としてチェック(決定)する同期式順序(論理)回路」として実現(設計)してみよう．この順序回路(装置)では，「在庫(数)＝0, 1, 2, 3 個(10進数表現)」を，この順で，FF-X,Yの各状態(出力) XY ＝00 (X＝0, Y＝0，以下同様), 01, 10, 11 (自然な2進数表現)で表す(状態割り当て)．また，入力 P は生産(Produce)操作，すなわち，P =1(CP ＝01)で上記モデルでの(b)(在庫を＋1)操作を示す．一方，入力 C は消費(Consume)操作，すなわち，C =1(CP ＝10)で上記モデルでの(c)(在庫を−1)操作を示す．C と P が同時に"0"(CP ＝00)のときは無操作(在庫状態は不変)である．C と P が同時に"1"(CP ＝11)のときの(次)在庫状態はドントケア"−"とする．次の(1)〜(8)の各問に答えなさい．

(1) 下記の拡大状態遷移表の「在庫^＋(次在庫状態)」列及びそれに従う X⁺, Y⁺ 列を埋めなさい．

(2) まず，この順序回路を(2個の)D-FFによって構成する．D-FFの入力要求表は表の通りであり，D-FFの場合には，(1)で作った拡大状態遷移表の X⁺, Y⁺ 列がそのままそれぞれ D_X , D_Y 列となることに注意して，この拡大状態遷移表の D_X , D_Y 列を解答欄の対応するカルノー図に写し，入力条件式 D_X, D_Y のそれぞれを2段論理最小化し，最小積和形論理式で示しなさい． カルノー図による操作はすべて解答として明記しなさい．

(3) (2)で求めた2段論理最小化した入力条件式 D_X , D_Y で構成する順序回路全体において，共有(共用)ゲートの存在によって，「2段」という各FF入力での時間最適化を保持したまま^†，さらなる空間最適化ができるかどうかについて，(2)の解答である最小積和形論理式を引用して論じなさい．ただし，「『2段』という時間最適化を保持したまま」^†とは，「ANDゲート(論理積項に対応)もORゲート(論理和項に対応)も，共有ゲートも含めて，多入力ゲート(多項演算項に対応)が使用できる場合は，それを優先して使用する(多入力ゲートを2入力ゲートに展開しない)」こととする．

(4) (2)で求めた D_X , D_Y の各最小積和形のうちで，ファクタリングを用いて多段論理最小化できるものがあれば，それらすべて(の結果)を最小形論理式で示しなさい．

(5) (2)でのカルノー図による2段論理最小化における解の導き(見つけ)方と，(4)によるファクタリングによる多段論理最小化における解の導き(見つけ)方とには，それを人間がやろうともコンピュータがやろうとも，論理的に大きな違いがある．この違いについて簡潔に説明しなさい．

(6) 次に，この順序回路を(2個の)JK-FFによって構成する．JK-FFの入力要求表は表の通りである．(i) これを用いて，(1)で作った拡大状態遷移表の右側の J_X, K_X, J_Y, K_Y 列を埋めて，拡大入力要求表として完成しなさい． (ii) この拡大入力要求表の J_X, K_X, J_Y, K_Y 列を解答欄の対応するカルノー図に写し，入力条件式 J_X, K_X, J_Y, K_Y のそれぞれを2段論理最小化し，最小積和形論理式で示しなさい． カルノー図による操作はすべて解答として明記しなさい．

(7) (i) (2)で求めた最小積和形論理式をテクノロジマッピングしてD-FFで構成するAND/OR回路と，(6)で求めた最小積和形論理式をテクノロジマッピングしてJK-FFで構成するAND/OR回路とについて，空間最適化の度合いの観点で2入力AND/ORゲート総数(ただし，2個のFFを構成するための分は除く)によって比較しなさい．また，(ii) (i)での定量的な比較をもとにして，D-FF とJK-FFとを，それぞれ単体(1個)の機能(能力)とそれぞれ単体(1個)を構成するのに必要な2入力AND/ORゲート総数との関係について，比較して論じなさい．

(8) (i) (6)で求めた最小積和形論理式をテクノロジマッピングしてJK-FFで構成するAND/OR回路を構成しなさい． (ii) (i)で得たAND/OR回路を回路変換によってNAND回路にしなさい．