[A] 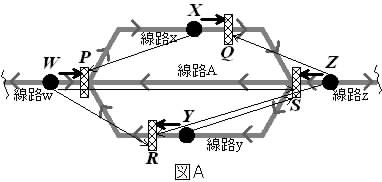図Aで示すように，5本の単線線路 A, w, x, y, z が(連結して)ある．線路 w と z では左右両方向進行可，A と y では左一方進行のみ，x では右一方進行のみ，それぞれ可である．また，線路 w, x, y, z 上には各1台の列車のみが存在できて，列車は，地点 W, X, Y, Z 上で，進行方向にある信号を確認するために停止する． ただし，線路 A では，列車は停止せずに左一方進行で w へ向かって通過する． いったん停止する列車は，地点 W では x を進行先とする右進行，X では z を進行先とする右進行，Y では w を進行先とする左進行，Z では A または y を進行先とする左進行，とする．従って，「地点 W, X, Y, Z 上に列車が停止(存在)しているか否か」は，各地点での列車の有無を表す論理値として，「列車無し」を"0"，「列車有り」を"1"とすることで，表現できる． また，W, X, Y, Z 地点にある各列車は，それぞれ，各地点にある進行方向側の信号 P, Q, R, S で，進行方向へ「進行不可」(「停止(赤)」，"0")か「進行可」(「進行(青)」，"1")かを確認(図Aでの太線矢印)する． ただし，「Z に有る( Z ＝1 )左進行列車は，W ＝0 ならば，Y に優先して( Y に列車が有っても，その列車は R の停止信号で停止したまま(*))，A を通過(経由)して w へ，W ＝1 かつ Y ＝0 ならば y へ，それぞれ自動的に分岐し左進行する」ように信号 S を「進行(青)」("1")に制御する．

このとき，各信号 P, Q, R, S を，進行先の線路上の地点W, X, Y, Z における各列車の(その時点での)有無(図Aでの細線矢印)のみによって，すなわち，「 P は X ＝0 (無)で"1"(青)，X ＝1 (有)で"0"(赤)，Q は Z ＝0 (無)で"1"(青)，Z ＝1 (有)で"0"(赤)，R は(*)を考慮して W ＝0 (無)かつ Z ＝0 (無)で"1"(青)，それ以外で"0"(赤)，S は W ＝0 (無)または Y ＝0 (無)で"1"(青)，それ以外で"0"(赤)」(制御規則A)で制御する．

地点 W, X, Y, Z に有る列車が確認する信号 P, Q, R, S の制御規則Aによる列車制御機構を，「W, X, Y, Z を入力， P, Q, R, S を出力とする4入力4出力組み合わせ回路」として最適化設計してみよう． 次の(1)〜(8)の各問に答えなさい．（論理積(AND)記号"・"は省略しなさい．）

(1) 制御規則Aの論理を下記の真理値表に写す． この真理値表の P, Q, R, S 列(左4列)を埋めなさい．

(2) (1)の真理値表から各出力 P, Q, R, S を解答欄のカルノー図に写し，それを用いて各出力 P, Q, R, S を2段論理最小化し，最小積和形論理式で示しなさい．カルノー図による操作はすべて解答として明記しなさい．

(3) (2)のP, Q, R, S それぞれが「多段論理最小化できるか否か」について，(2)の解答を引用して，簡潔に述べなさい．

(4) (2)の P, Q, R, S を1つにまとめた4出力論理回路における「共用(共有)AND/ORゲートの有無」について，(2)の解答を引用して，簡潔に述べなさい．

(5) 「地点 W, X, Y, Z に列車が無ければ，各地点で確認すべき各信号 P, Q, R, S は，この順で，無意味である」を「 W ＝0 ならば信号 P はドントケア"−"，同様に，X ＝0 ならば信号 Q はドントケア"−"，Y ＝0 ならば信号 R はドントケア"−"，Z ＝0 ならば信号 S はドントケア"−"」($)とできる．この論理関係($)で(1)を修正して，下記の真理値表の P, Q, R, S 列(右4列)を埋めなさい．

(6) (5)の真理値表から各出力 P, Q, R, S を解答欄のカルノー図に写し，それを用いて各出力 P, Q, R, S を2段論理最小化し，最小積和形論理式で示しなさい．カルノー図による操作はすべて解答として明記しなさい．

(7) 「W, X, Y, Z のすべての地点にも列車が存在する(有る，"1")場合，信号 P, Q, R, S はすべて"0"(赤)になり，どの列車も停止したまま進行できない」という状態(「デッドロック」という)に陥る． この「デッドロック状態」の条件と結果を示す論理関係を簡潔な論理式で示しなさい．

(8) (2)と(6)の結果を比較して得る「各地点での列車(の有無)と信号との論理関係」(制御規則A以外で)について，簡潔な日本語で述べなさい．

[B] 図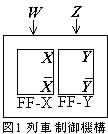Bは，図Aから4台の信号を取り除いた外は列車や線路に関する仕様(#)が図Aとまったく同じ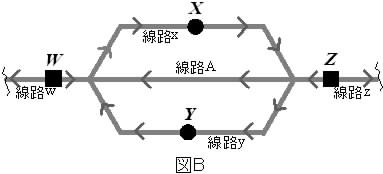，連結単線線路 A, w, x, y, z である．今度は，ある時刻(ビットタイム) t での地点 W, X, Y, Z における列車の有無のみで，次時刻 t⁺ での地点 X⁺, Y⁺ での列車の有無(進行状況)を集中制御･指令する自動列車制御機構について考える．この列車制御機構を「入力を W, Z ，状態を2個のフリップフロップ(FF-X, FF-Y)の状態(出力) X, Y とする同期式順序回路」(図1 )として最適化設計してみよう． すなわち，この順序回路では，入力 W, Z と現状態 X, Y だけで，次状態 X⁺, Y⁺ への状態遷移を決定する．そして，入力 i を i₀, i₁, i₂, i₃ と記号で表現し，この順で，入力 WZ ＝00 (W＝0, Z＝0，以下同様), 01, 10, 11 に割り当てる．また，現状態 s と次状態 s⁺ を s₀, s₁, s₂, s₃ と記号で表現し，この順で，FF-X,Yの各状態(出力) XY ＝00 (X＝0, Y＝0，以下同様), 01, 10, 11 に割り当てる(状態割り当て)．ここで，「仕様(#)の下で列車を制御すると，記号表現による状態遷移図が右図となる」ように，この列車制御機構を設計する．次の(1)〜(7)の各問に答えなさい．（論理積(AND)記号"・"は省略しなさい．）

(1) 記号表現した状態遷移図によって，下記の拡大状態遷移表の s⁺ 列を埋めなさい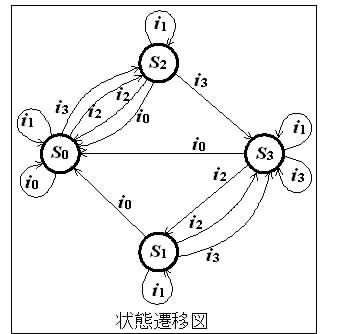．さらに，各 s⁺ を X⁺, Y⁺ に展開して X⁺, Y⁺ 列を埋めなさい．

(2) まず，この順序回路を(2個の)D-FFによって構成する．D-FFの入力要求表は表1の通りであり，D-FFの場合には，(1)で作った拡大状態遷移表の X⁺, Y⁺ 列がそのままそれぞれ D_X , D_Y 列となることに注意して，この拡大状態遷移表の D_X , D_Y 列を解答欄の対応するカルノー図に写し，入力条件式 D_X, D_Y のそれぞれを2段論理最小化し，最小積和形論理式で示しなさい． カルノー図による操作はすべて解答として明記しなさい．

(3) (2)で求めた D_X , D_Y の各最小積和形のうちで，ファクタリングを用いて多段論理最小化できるものがあれば，それらすべて(の結果)を最小形論理式で示しなさい．

(4) 次に，この順序回路を(2個の)JK-FFによって構成する．JK-FFの入力要求表は表1の通りである．この入力要求表を用いて，(1)で作った拡大状態遷移表の右側の J_X, K_X, J_Y, K_Y 列を埋めて，拡大入力要求表として完成しなさい．

(5) (4)の拡大入力要求表の J_X, K_X, J_Y, K_Y 列を解答欄の対応するカルノー図に写し，入力条件式 J_X, K_X, J_Y, K_Y のそれぞれを2段論理最小化し，最小積和形論理式で示しなさい． カルノー図による操作はすべて解答として明記しなさい．

(6) (2)で求めた最小積和形論理式 D_X , D_Y を制御入力とするD-FFで構成するAND/OR回路と，(5)で求めた最小積和形論理式 J_X, K_X, J_Y, K_Y を制御入力とするJK-FFで構成するAND/OR回路とについて，空間最適化の度合いの観点で2入力AND/ORゲート総数(ただし，2個のFFそのものを構成するための分は除く)によって比較することによって，「D-FF とJK-FFそれぞれ単体(1個)の機能(能力)」について，比較して論じなさい．

(7) [A]の(7)で考察した「W, X, Y, Z のすべての地点に列車が存在する(有る，"1")」場合も，[B]の列車制御機構では，(実際はともかく)仕様上では，[A]の(7)で指摘したような「デッドロック状態」は発生しない．この理由について，この順序回路を([A]の)組み合わせ回路と比較する観点で，また，状態遷移図を引用して，簡潔に述べなさい．